Comme promis dans le dernier article, voici un jeu de plateau pour entraîner les élèves aux premiers calculs, par la recherche d’équivalences additives. Un moyen ludique pour mémoriser les fameuses « tables d’additions », si difficiles à apprendre.

 

---

J’ai conçu le jeu présenté aujourd’hui comme une synthèse du travail décrit dans le précédent article. C’est pourquoi je vous invite à consulter celui-ci avant d’aller plus loin, afin que mes explications ne vous semblent pas obscures. C’est ici.

Matériel

— Une piste qui autorise les déplacements en tous sens.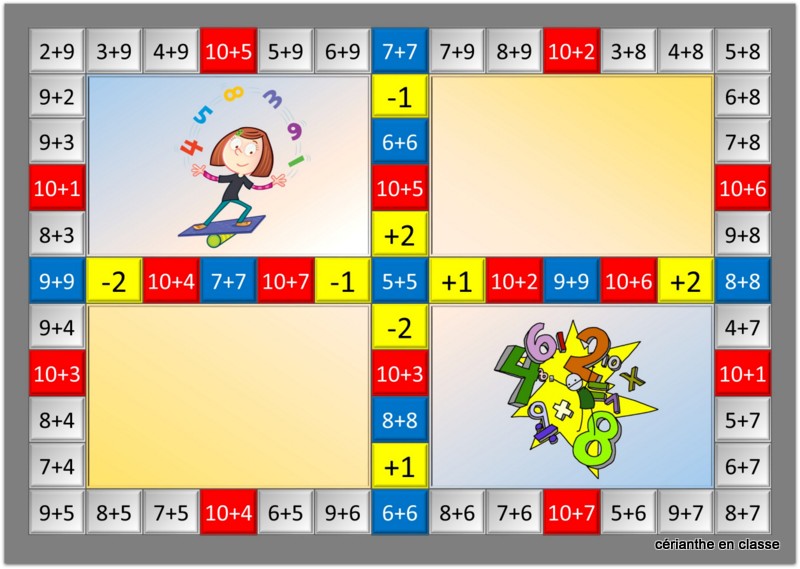

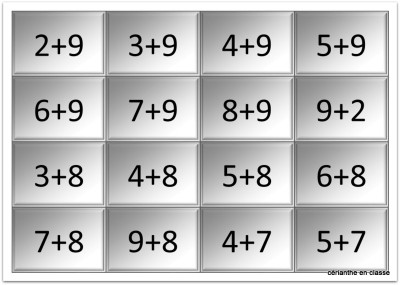
— Une série de trente deux cartes grises, sur lesquelles ne figurent que les sommes du tableau de Pythagore supérieures à dix.

 

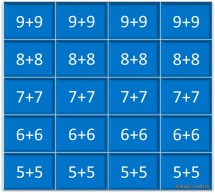
— Une série d’étiquettes bleues : ce sont les doubles dont le résultat est supérieur à dix également.

 

 

 

— Une série d’étiquettes jaunes : elles ne comportent que les mentions : +1 , -1 +2 et -2.

Le but du jeu

Le joueur doit trouver une équivalence additive à la somme figurant sur la carte grise qu’il a obtenue, et aller la chercher sur la piste. Par exemple s’il a devant lui la carte 7+5, il doit se rendre sur la case 10+2 de la piste. Ou sur 6+6. Il peut aussi faire le choix d’aller chercher l’étiquette 7+7, auquel cas il devra ensuite se placer sur une case -2. Chaque équivalence réalisée rapporte des points, correspondants aux unités de la somme. Dans le cas de 7+5, le joueur gagne deux points (le 2 de 12). Pour 8+9, le joueur récoltera 7 points (le 7 de 17). Celui qui a obtenu le plus de points à la fin de la partie a gagné.

Règle du jeu

Au départ de la partie, une carte-somme est distribuée à chaque élève puis le matériel est disposé sur le plateau comme sur l’image. Les joueurs se placent sur la case correspondant à leur somme, et le premier lance le dé. À partir de là, deux options sont possibles :

Règle initiale

Comme expliqué plus haut, les joueurs doivent se rendre sur la case équivalente à leur somme : soit sur une case rouge (10+…), soit sur une bleue (les doubles). chacun avance à son tour au gré des tirages du dé. Arriver pile sur la case désirée peut être plus ou moins long. Quand il y parvient, le joueur marque ses points et remet la carte-somme dans la pile. Il doit ensuite aller en chercher une autre en se déplaçant sur la piste.

Précisions :

– Imaginons qu’un joueur doive trouver l’équivalence de 8+6. S’il se place sur 7+7 (case bleue) l’équivalence est alors réalisée, il marque aussitôt ses points. Par contre, s’il se place sur 6+6, l’équivalence est seulement en cours de réalisation car il doit encore se rendre sur une case +2. Dans ce cas, il prend l’étiquette 6+6 pour attester qu’il est bien passé sur la case. Dès qu’il arrivera sur la case +2, l’équivalence sera réalisée, il marquera ses points et remettra sa carte et son étiquette au centre du jeu. Pour autant, rien ne l’empêche de s’arrêter sur la case 10+4 ou 7+7 en cours de route.

– Le principe des points est intéressant car les élèves sont amenés à effectuer d’autres calculs au cours de la partie. C’est donc un entraînement supplémentaire. Mais vous pouvez remplacer cette contrainte par la remise de jetons à chaque équivalence réalisée.

Règle étendue

Pour cette version, vous aurez besoin des étiquettes rouges correspondant aux sommes du type : D+U. Ici en effet, le joueur reçoit la carte-somme ou l’étiquette correspondant à la case sur laquelle il s’arrête à chaque tour. Il doit effectuer ses équivalences en fonction de ce qu’il a devant lui. Les possibilités de combinaisons sont à la fois plus larges, plus rapides et plus faciles. Cette variante est plus vivante et oblige souvent l’élève à varier ses stratégies de calcul. Je la réserve cependant à des élèves un peu plus mûrs car il faut savoir traiter plusieurs informations en même temps.

 

cartes du qui compte vite          piste du qui compte vite