 Faire mémoriser les tables d’addition est une véritable gageure, que ce soit au CP ou au CE1. Je vous propose ci-dessous une progression qui amènera vos élèves, en douceur et sans stress, à bien les connaître. Finies les longues litanies récitatives qui ne mettent pas de sens, donc n’aident pas à retenir. Les fiches mémos jointes permettront de reprendre le travail à la maison.
Faire mémoriser les tables d’addition est une véritable gageure, que ce soit au CP ou au CE1. Je vous propose ci-dessous une progression qui amènera vos élèves, en douceur et sans stress, à bien les connaître. Finies les longues litanies récitatives qui ne mettent pas de sens, donc n’aident pas à retenir. Les fiches mémos jointes permettront de reprendre le travail à la maison.
Je vous le disais dans un article précédent, ne pas connaître « ses tables d’addition » finit par être préjudiciable quand il faut faire des calculs un peu plus complexes du type (au CE1) : 38+46. Ou même 56+7. Je suis actuellement des élèves de CM1 qui se noient au moindre calcul. Ils perdent un temps fou à compter sur leurs doigts et souvent ne savent plus où ils en sont. J’ai dû me rendre à l’évidence : inutile de se pencher sur la valeur positionnelle des chiffres pour aider aux calculs tant que les tables ne sont pas sues. J’ai donc été amenée à réfléchir sur une méthode de mémorisation basée sur l’observation des termes d’une somme.
Étape 1 : +0, +1
Pour mes séances, j’utilise les cartes additives que vous trouverez ici. Au départ, je montre la pile de cartes en énonçant l’objectif final : être capable de donner le résultat de chaque somme le plus rapidement possible.
 Au préalable, je sélectionne toutes les sommes du type +0, +1 et leur inverse. Puis je fais une petite séance de « calcul flash ». Évidemment, les élèves s’esclaffent : « Pff, trop facile ! » Je leur demande alors de formuler en termes clairs pourquoi c’est si simple :
Au préalable, je sélectionne toutes les sommes du type +0, +1 et leur inverse. Puis je fais une petite séance de « calcul flash ». Évidemment, les élèves s’esclaffent : « Pff, trop facile ! » Je leur demande alors de formuler en termes clairs pourquoi c’est si simple :
– +0 ça veut dire qu’on n’ajoute rien. Donc on garde le nombre de l’addition.
– +1 veut dire qu’on obtient le nombre qui suit.
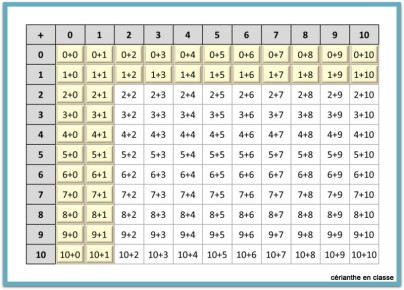
À ce moment, je sors une table de Pythagore comme celle ci-contre en expliquant qu’elle contient toutes les additions des nombres de zéro à dix. Et je propose de colorier les cases correspondant aux sommes +0 et +1. Cela signifie que ces sommes ne posent pas de problème de calcul.
Étape 2 : +2 et +3
 Même démarche : je sélectionne d’abord toutes les cartes additives avec +2. Assez vite, je demande à chacun de donner sa méthode de calcul. Comme j’ai à faire à des élèves de bonne volonté, je les entends invariablement m’expliquer, par exemple pour 9+2 :
Même démarche : je sélectionne d’abord toutes les cartes additives avec +2. Assez vite, je demande à chacun de donner sa méthode de calcul. Comme j’ai à faire à des élèves de bonne volonté, je les entends invariablement m’expliquer, par exemple pour 9+2 :
– Je mets 9 dans ma tête et j’ajoute 2 sur mes doigts.
– D’accord. Mais tu es obligé(e) de compter sur tes doigts ? Ajouter 2, c’est à dire avancer de 2 peut se faire mentalement. Essaie !
Et là, tout le monde acquiesce. On s’entraîne donc dans un premier temps à effectuer les calculs à haute voix, ce qui donne pour 9+2 : « Neuf, dix onze ». Une fois que la démarche est intégrée, elle doit pouvoir être utilisée mentalement. Je propose à cet effet quelques exercices de rapidité :
– Compter de deux en deux à partir d’un nombre donné, sur le mode du furet.
– Une carte-nombre est présentée à un élève qui doit instantanément donner le nombre N+2. (J’ai toujours un jeu de cartes-nombres de 0 à 99 avec moi. Si vous n’en avez pas, voici un fichier à photocopier. Les cartes sont sans fioritures…) cartes nb de 0 à 100
Après quoi on revient aux cartes additives avec un petit tour de calcul flash.
La démarche est ensuite reprise avec +3.
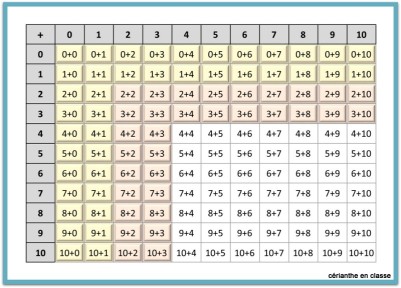
Pour finir, les élèves sortent leur table de Pythagore et peuvent colorier toutes les sommes du type +2 et +3. À ce stade, on peut faire remarquer que plus de la moitié du tableau est déjà coloriée.
Étape 3 : les doubles jusqu’à dix (5+5)
Normalement, les élèves les connaissent déjà, au moins jusqu’à 5+5.
— Dans un premier temps, j’étale sur la table les cartes suivantes : 2+3, 3+4, 4+5, 5+6 et leur inverse, puis je demande de trouver la particularité de ces sommes. Elles sont constituées de deux nombres qui se suivent. L’objectif est d’amener les élèves à remarquer qu’elles sont proches des doubles, c’est-à-dire que 3+4, c’est (3+3)+1. Ou bien que 5+4, c’est (5+5)-1.
— Dans un deuxième temps, j’étale les cartes 1+3, 2+4, 3+5, 4+6 et leur inverse, puis je pose la même question : qu’est-ce que ces sommes ont en commun ? Il y a un écart de 2 entre les nombres. Donc si j’enlève 1 au plus grand des deux et que je l’attribue au plus petit, j’obtiens un double. Évidemment, ce sont les élèves qui doivent trouver la méthode, par un jeu de questions et/ou manipulations. L’image ci-dessous est plus parlante. Selon les élèves, la manipulation sera ou non nécessaire. Si elle l’est, je n’hésite pas à la faire faire pour chaque somme. 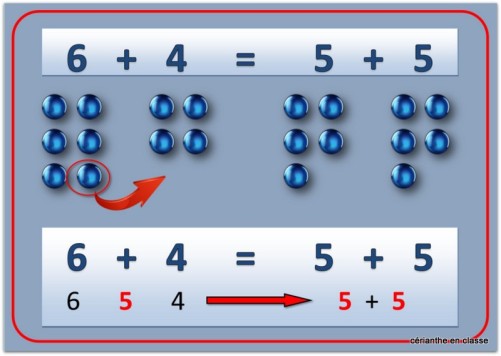
Mais certains élèves préfèrent la méthode double+2. Par exemple, 4+6=(4+4)+2.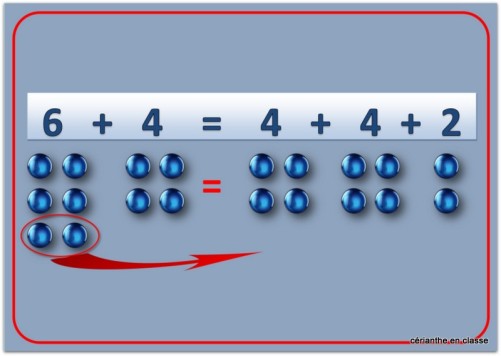
La séance se termine par un exercice de calcul rapide en deux temps. Toutes les cartes étudiées sont mélangées et les élèves en tirent une à tour de rôle. Ils doivent d’abord reformuler la règle issue des observations se rapportant à leur carte puis effectuer le calcul oralement. Ensuite on passe au calcul flash : pour gagner en rapidité, la démarche doit cette fois rester mentale.
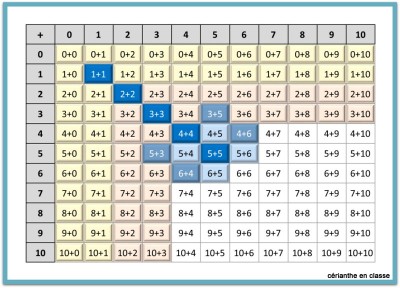
Et bien sûr, on continue à remplir le tableau d’addition.
Pour la séance suivante, il est demandé aux élèves d’apprendre les doubles jusqu’à 9+9.
Étape 4 : tous les doubles
Le déroulement est exactement le même que pour la séance précédente.
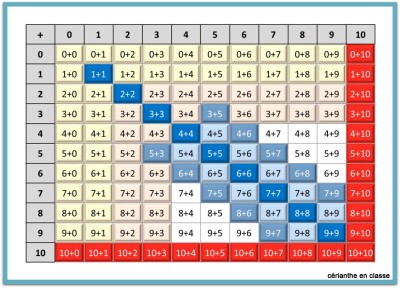 Après avoir colorié les cases du tableau relatives au travail du jour, je mélange toutes les cartes correspondant aux sommes étudiées depuis le début. Sans rien dire, j’ajoute les 10+… et les …+10 au complet. Si on se rapporte au tableau, on voit que les élèves en connaissent déjà la majeure partie. Après un temps de calcul flash, je leur fais remarquer qu’ils peuvent compléter la dernière ligne et la dernière colonne du tableau.
Après avoir colorié les cases du tableau relatives au travail du jour, je mélange toutes les cartes correspondant aux sommes étudiées depuis le début. Sans rien dire, j’ajoute les 10+… et les …+10 au complet. Si on se rapporte au tableau, on voit que les élèves en connaissent déjà la majeure partie. Après un temps de calcul flash, je leur fais remarquer qu’ils peuvent compléter la dernière ligne et la dernière colonne du tableau.
Étape 5 : +9
Cette fois, ce sont toutes les sommes avec 9 qui sont étalées sur la table. Les élèves commencent à être habitués à jongler avec les chiffres. Ils sont donc aptes à remarquer très vite que 9 est proche de dix. Or, il est beaucoup plus facile d’effectuer un calcul avec +10 qu’avec +9. On va donc réaliser les mêmes permutations que lors du travail sur les doubles, avec le même travail d’entraînement.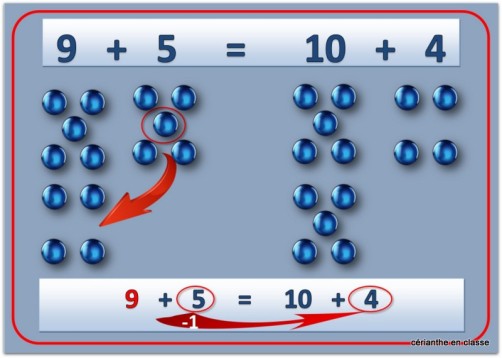
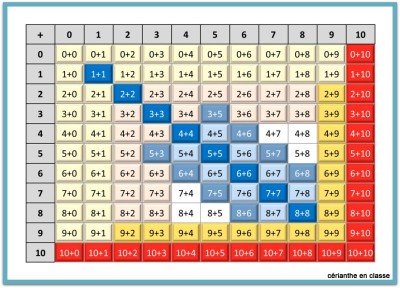 Quand on remplit la grille, on voit qu’il reste peu de sommes à travailler. On arrive presque au bout ! Pour la séance suivante, justement, il est demandé aux élèves de revoir les compléments à dix. On peut leur faire remarquer que les cases correspondantes sont déjà coloriées, ce qui signifie que le travail de mémorisation ne devrait pas poser de problème. Pour autant, j’insiste sur le fait que cette mémorisation doit être automatique, comme pour des doubles.
Quand on remplit la grille, on voit qu’il reste peu de sommes à travailler. On arrive presque au bout ! Pour la séance suivante, justement, il est demandé aux élèves de revoir les compléments à dix. On peut leur faire remarquer que les cases correspondantes sont déjà coloriées, ce qui signifie que le travail de mémorisation ne devrait pas poser de problème. Pour autant, j’insiste sur le fait que cette mémorisation doit être automatique, comme pour des doubles.
NB : Au besoin, on peut consacrer une ou deux séances au travail d’automatisation des compléments à dix. Je vous renvoie à l’article qui lui est consacré, ici.
Étape 6 : utiliser les compléments à dix
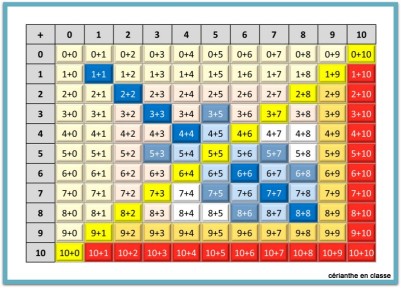
Arrivés à ce stade, il reste peu de cases non coloriées dans le tableau. Les cartes-sommes correspondantes sont étalées sur la table et il est demandé aux élèves de trouver une technique de calcul. Bien entendu, il va s’agir de compléter le plus grand à dix.
J’ai dans mon groupe de CM1 une élève qui a de réels problèmes de mémorisation. Toutes les opérations mentales de calcul sont vraiment compliquées pour elle. À tel point qu’avec elle, il faut en repasser par les doigts. On peut cependant essayer de gagner du temps en utilisant les connaissances acquises. Par exemple pour 8+6 : elle prépare six doigts et commence à surcompter à partir de huit. Dès qu’elle arrive à dix, elle n’a plus qu’à regarder combien de doigts ouverts il lui reste. Il suffit ensuite de calculer 10+ le nombre de doigts restants.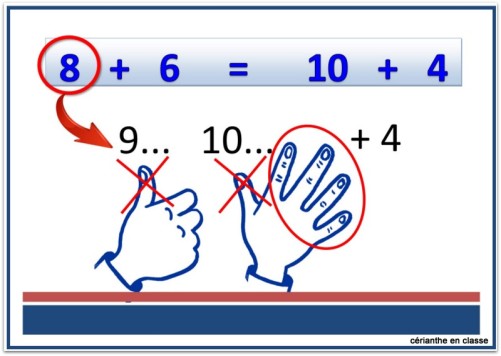
Trace écrite
Je me suis aperçue dans mes groupes que certains élèves ont tendance à s’accrocher à une méthode au point d’en oublier les autres, même quand elles sont plus faciles. J’ai donc concocté des fiches-mémos qui servent pendant la séance. Une carte est tirée au hasard et le groupe doit trouver toutes les manières possibles de faire le calcul, en se référant aux fiches. Prenons l’exemple de 8+6 : c’est 10+4 mais aussi 7+7 ou encore (6+6)+2. fiches mémos tables d’addition
Pour ceux qui le souhaitent, je joins les fiches bleues à afficher comme soutiens temporaires aux techniques décrites : technique d’addition 1
Ici, un fichier avec deux tableaux de Pythagore : un rempli et un vierge, en fonction de votre projet d’utilisation.
NB : après demande, j’ai ajouté un troisième tableau, celui des additions.
La semaine prochaine, vous aurez droit à un grand jeu de synthèse qui reprendra les principales techniques étudiées. À bientôt !





Bonjour,
Merci pour ce partage. Je faisais des recherches pour créer un carnet de calcul mental pour des CM1 mais en reprenant les bases car certains ont un petit niveau CE1.
Et bien, j’ai adorée la stratégie pour calculer deux nombres séparés de 2 (faire le double du nombre qui est au milieu). C:est la première fois que je la vois et en trace écrite. Bravo pour ton travail. J’adore.
J’aimeJ’aime
Merciii pour ce déroulé, je vais mettre cela en place pour mes élèves les plus fragiles.
J’aimeJ’aime
L’explication des tables d’addition prend combien de temps à être expliquer en classe
J’aimeJ’aime
Bonjour Layal,
il faut évidemment compter plusieurs séances, avec entraînements. Mais ça va de plus en plus vite, une fois que le processus est compris.
Je précise que ce n’est pas du temps perdu, au contraire, vous en gagnerez par la suite au moindre calcul et surtout, la méthode permet aux élèves « d’agir » sur les nombres.
J’aimeJ’aime
Bonjour,
Merci pour toutes ces explications, c’est tellement clair et bien expliqué. J’ai tout imprimé pour tester rapidement avec ma fille. J’aurai juste voulu savoir s’il était possible d’avoir la table de Pythagore mais avec les additions afin qu’elle puisse les colorier.
Merci d’avance.
J’aimeJ’aime
Bonjour Radia,
Merci pour votre commentaire. Je viens de vérifier l’article. Je vais voir si je peux joindre la table de Pythagore au fichier. Sinon, en attendant, vous pouvez remplir vous-même le tableau vierge.
J’aimeJ’aime
RE-bonjour radia,
ça y est, j’ai modifié l’article. Vous trouverez le tableau des additions dans le fichier « Tableau de Pythagore ».
Bonne journée à vous
J’aimeJ’aime
Merci énormément pour cette belle explication. Je m y attaque avec ma fille..
J’aimeJ’aime
Merci Tania.
Vous pouvez aussi consulter cet article qui vous apportera des idées de jeux d’entraînement avec des dés.
En espérant que votre fille apprendra tout en y trouvant du plaisir.
J’aimeJ’aime
A la recherche d’idées pour faire apprendre les tables, je suis tombée par hasard sur votre site.Quel beau travail, de clarté, de précision ! merci mille fois, je redoute toujours un peu ce moment, l’apprentissage des tables. Mais je crois qu’avec votre démarche, ça va être plus facile et surtout plus de sens pour les élèves. Encore merci pour ce partage.
J’aimeAimé par 1 personne
Bonjour Marnie,
Oui l’apprentissage des tables peut être aussi ennuyeux pour l’enseignant que pour les élèves si on n’y met pas du sens. J’avais élaboré cette technique pour des élèves en difficultés, alors avec une classe hétérogène, ça devrait passer comme une lettre à la poste ! Bonne suite à vous !
J’aimeJ’aime
Un immense merci pour ce partage. Ayant une classe de CE1 l’année prochaine, après plusieurs années en maternelle, vos outils partagés vont m’être très précieux pour élaborer les stratégies et procédures mentales chez mes futurs élèves.
J’aimeJ’aime
Mille mercis pour le partage!
J’ai trouvé plein de choses intéressantes pour aborder les mathématiques (décompositions additives,, compléments à 10 et bien sûr les tables d’addition !!!) . C’est réfléchi et très clair, ça me parle !
Ça va me servir dans ma façon d’amener certaines notions et je vais très certainement utiliser les jeux dans mes ateliers .
Merci encore et bonne fin d’année !
J’aimeJ’aime
Ce commentaire me fait vraiment plaisir, merci Marie !
Il est vrai que le fait de travailler essentiellement avec des élèves en difficultés oblige à penser la pédagogie… autrement ! Et tout le monde en profite.
Bonne fin d’année à vous aussi !
J’aimeJ’aime
Bonjour,
Merci pour ce partage! Effectivement les tables d’addition ne sont pas faciles à faire apprendre. J’adore votre démarche, elle correspond en tout point à ma façon de penser. Merci à vous.
J’aimeJ’aime
Génial, merci Galthie.
Quelle que soit la méthode, les élèves auront de toute façon besoin de temps pour mémoriser quelque chose qui, en soi, n’a guère de sens. Or, on sait comme la dimension du sens est importante dans la mémorisation. Donc même en y apportant de la réflexion, il faut savoir se montrer patient. La répétition étant aussi un facteur essentiel, pourquoi ne pas passer par le jeu qui augmente l’implication ? J’ai rédigé dernièrement des articles sur les jeux mathématiques avec peu de matériel, allez y faire un tour et n’hésitez pas à me faire des retours.
Bonne fin d’année à vous.
J’aimeJ’aime